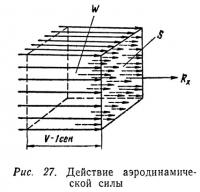
Полная аэродинамическая сила, например, возникает при набегании потока воздуха на пластинку, расположенную перпендикулярно к направлению потока. Эта сила препятствует движению пластинки (если пластинка движется в неподвижном воздухе) или толкает ее (если пластинка находится в неподвижном состоянии, а поток воздуха набегает на нее). Аэродинамическую силу, действующую так, как показано на рис. 27, называют силой лобового сопротивления X, поскольку она направлена навстречу потоку, «в лоб».
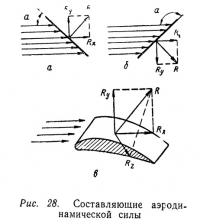
Если пластинку наклонить к набегающему потоку под некоторым углом (рис. 28, а), то возникает составляющая полной аэродинамической силы, которая называется подъемной силой У. Эта сила поднимает ракету или поддерживает ее горизонтальный полет. Однако подъемная сила может не только поднимать, но и быть направленной вниз. Так, на пластинке, расположенной по отношению к набегающему потоку под положительным углом (рис. 28, а), подъемная сила направлена вверх, а на пластине, подставленной под отрицательным углом (рис. 28, б), подъемная сила направлена вниз.
Рассмотрим аэродинамику крыла (в такой же степени это относится и к наибольшему поперечному сечению модели ракеты). При набегании потока на крыло (рис. 28, в) возникает сила лобового сопротивления X и подъемная сила Y. Если крыло повернуть относительно продольной оси х, то возникнет третья сила — боковая Z. Она будет действовать вправо или влево в зависимости от того, как повернуто крыло к потоку.
Разумеется, все эти силы условные, в действительности существует только одна — полная аэродинамическая сила. Такое условное разделение вызвано необходимостью, так как дает возможность опытным путем заранее определить направление сил и, сложив их по правилу параллелограмма, получить полную аэродинамическую силу.
Сила лобового сопротивления равна:
Аналогично выглядит и формула подъемной и боковой силы:

Коэффициенты лобового сопротивления Сх, подъемной силы Су и боковой силы Сz по своей природе аналогичны друг другу. Расчет коэффициентов является трудной задачей, их определяют приближенно, а затем уточняют по результатам опытов в аэродинамических трубах.
Модель ракеты помещают в аэродинамическую трубу, через которую протекает поток воздуха с определенной скоростью, и фиксируют действующие на нее силы, после чего подсчитывают аэродинамические коэффициенты, в том числе и значение Сzx.
Имеются и другие методы определения значения Сх, например, путем сравнения с уже существующими моделями ракет. Поэтому модель ракеты необходимо сохранять той формы, которая проходила продувку в аэродинамической трубе.
Коэффициент лобового сопротивления Сх — безразмерная величина, зависящая в основном от формы ракеты и скорости полета. Так как коэффициент лобового сопротивления для дозвуковых скоростей остается примерно постоянным, а в ракетном моделизме мы имеем дело именно с такими скоростями, то влияние скорости на Сх учитывать не будем.
Величина коэффициента зависит также от угла атаки, от состояния поверхности модели ракеты и ряда других причин, которые мы также рассматривать не будем.
Большое внимание на величину Сх оказывает форма модели ракеты. С точки зрения аэродинамики лучшей является форма, при которой величина Сx наименьшая. Поэтому, с целью получения минимально возможного для данного диапазона скоростей сопротивления, надо стремиться к оптимальной форме модели ракеты.
Удлинения моделей ракет λ=l/d возможны в пределах от 8 до 30, при среднем диаметре 25 мм. Значение коэффициента Сх для этой геометрии можно принять от 0,25 до 0,4, причем меньшее значение Сх будет соответствовать оптимальному удлинению модели ракеты: λ≈22.
Площадь поперечного сечения ракеты S подсчитывается по максимальному диаметру корпуса D: